Stress Level Using Data Analysis Continuous Wavelet Transform Scholarly Articles

1. Introduction

A certain amount of heavy metals (e.g., copper) in plants is essential for building enzymes and proteins, which are beneficial to plant growth and development [1]. However, the uptake of excessive heavy metals from contaminated soils, waste water, or road dusts may disrupt the homeostatic mechanism of plant photosynthesis and stimulate the formation of oxidative stress, resulting in leaf injury, growth inhibition, and yield reduction [1,2,3,4]. In terrestrial ecosystems, the concentration of heavy metals in plant leaves is an important indicator of pollution status in surrounding environment [5,6]. It is, therefore, important to monitor the spatial and temporal dynamics of heavy metal concentrations in leaves for early warning of heavy metal pollution and understanding the ecosystem responses to heavy metal variations in specific environments.

Hyperspectral remote sensing is a valid alternative to traditional ground-based methods, and it has been widely used to quantify the biophysical (e.g., leaf area index and net primary productivity) [7] and biochemical (e.g., chlorophyll and nitrogen) [8,9,10] properties of plants at the leaf, canopy, and landscape levels. Numerous studies have focused on the retrieval of the spectrally active biochemical properties of plants (e.g., water, chlorophyll, and nitrogen) using physical or statistical models [8,9,10,11,12,13,14,15,16,17,18,19,20]. In contrast, much less progress has been made to estimate foliar heavy metal concentrations [21,22,23,24,25], which may be due to their very low concentrations in plant leaves (e.g., normally 5−30 mg∙kg⁻¹ for Cu) [26] and absence of evident physical absorption features existing for major constituents (e.g., water, chlorophyll, and starch) [27]. This makes it impossible to predict heavy metal concentrations directly from hyperspectral data. Several studies with controlled experiments have found that chlorophyll concentrations in plant leaves tend to decrease with increasing heavy metal stress levels [4,23]. The reason for this relationship is that heavy metals are known to interfere with chlorophyll synthesis [4,28]. Consequently, the heavy metal stress in plant leaves would characteristically change the leaf reflectance spectrum, such as increasing reflectance over visible wavebands, decreasing reflectance over near-infrared wavebands and shifting the red edge position to shorter wavebands [23,29]. Hence, heavy metal concentrations could be theoretically predicted by capturing the indirect change of reflectance spectra caused by the decrease of chlorophyll concentration in plant leaves.

In order to effectively capture the abovementioned change of reflectance spectra under heavy metal stress, some spectral parameters, such as vegetation index [22], band depth parameter [24], and position parameter [23,24], were employed for foliar heavy metal estimation. However, none of these studies have attempted to derive an area parameter (the sum of reflectance over a sensitive spectral region) from vegetation reflectance spectra. This parameter can cover more spectral information than two-band or three-band vegetation index, and it has been proven to provide a more highly accurate model than position parameters [30]. Delegido et al. [18] demonstrated the successful application of an area parameter in estimating foliar chlorophyll concentrations of heterogeneous crops. For this reason, area parameters may be suitable for quantifying trace heavy metals without evident absorption features.

Under natural conditions, heavy metal concentrations in plant leaves might not be high enough to trigger the significant change of vegetation reflectance spectra, hence, a method that can be used to enhance the potential subtle spectral changes is needed. Several studies have employed wavelet transform (WT) to overcome this problem [22,31], because WT can preserve the peaks and valleys among spectral signatures and magnify subtle spectral features [22,32]. WT breaks up a signal into a set of shifted and scaled versions of the original (or mother) wavelet, resulting in approximation (low-pass filter) coefficients and detail (high-pass filter) coefficients at various decomposition levels [33,34]. WT also has good performances in spectral denoising and smoothing [35] and spectral dimension reduction [36]. WT has been used successfully in many fields of remote sensing, such as image processing [37], identification of vegetation [38], mapping [39], and quantification of biochemical parameters in plant leaves, such as chlorophyll concentration [9,40], water content [15], and heavy metal concentrations [22].

The spectral parameters used for quantifying biophysical and biochemical properties of plants are generally derived from original, derivative, or continuum-removed reflectance. Few of the previous studies have documented spectral parameters (especially area parameters) derived from the WT analysis of vegetation reflectance. Liu et al. [22] were the first to attempt to estimate Cu and Cd concentrations in rice leaves using a wavelet-based spectral parameter. However, this type of estimation is still at the exploratory stage and requires more investigation and test with other species. Further, the methodology of developing a wavelet-based spectral parameter, such as how to select the optimal decomposition level and extract the optimal spectral region for area parameter construction, has not been well described for reference in existing studies.

With samples and reflectance spectra of plants collected under field conditions, this study aimed to (i) explore the relationship between Cu and chlorophyll concentration in Carex (C. cinerascens) leaves, (ii) describe a wavelet-based area parameter from canopy reflectance of Carex to enhance the subtle spectral changes related to chlorophyll concentration under Cu stress, and use it to indirectly estimate foliar Cu concentrations, and (iii) compare the performance of the wavelet-based area parameter to that of some classical chlorophyll-related and wavelet-based spectral parameters in Cu estimation.

2. Materials

2.1. Study Area

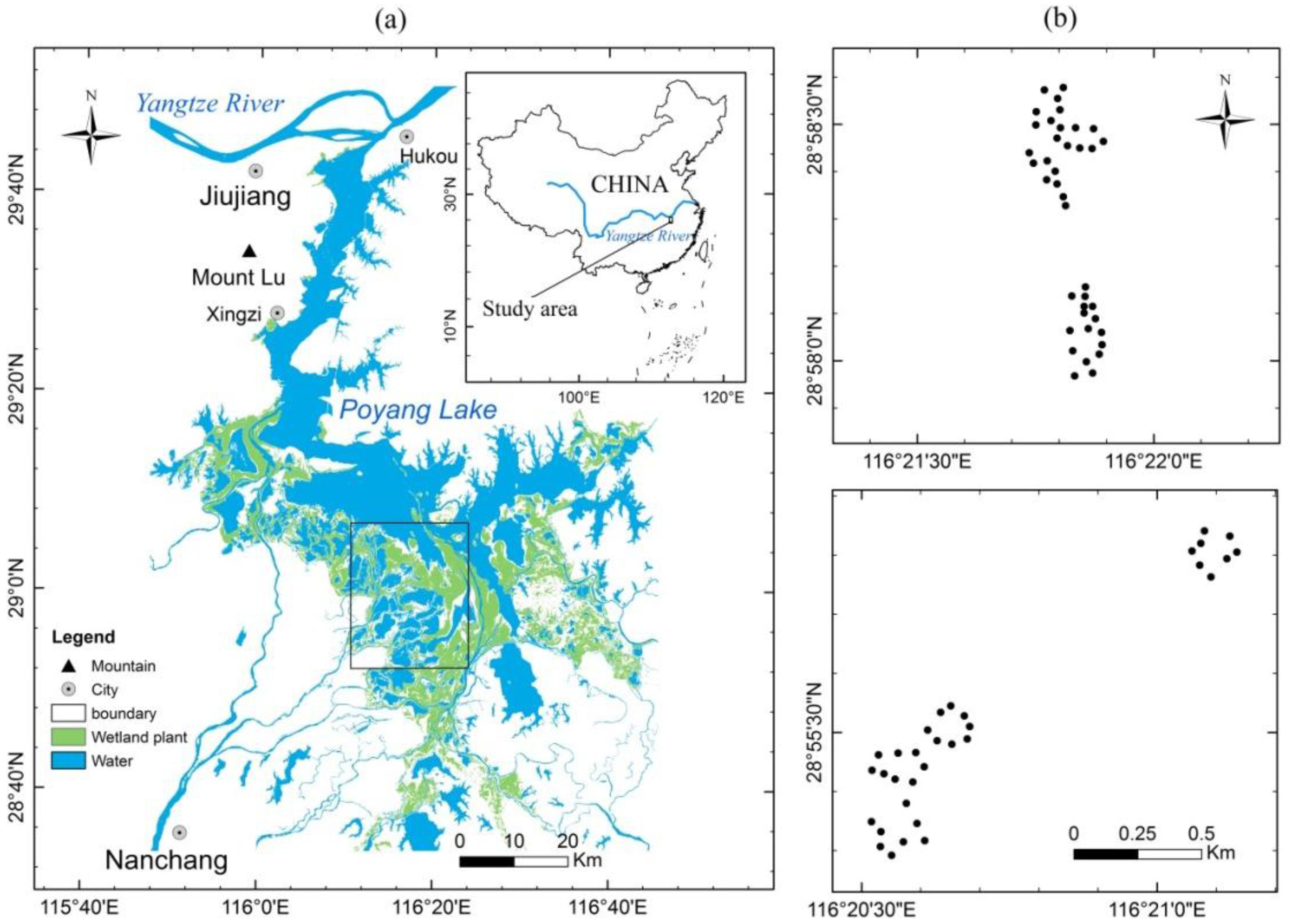
The study area is located in Poyang Lake (28°52′21′′N−29°06′46′′N, 116°10′24′′E−116°23′50′′E), China (Figure 1a). Poyang Lake is the largest fresh lake in China. Carex (C. cinerascens) is the dominant wetland species in Poyang Lake, and it is the main food source of many over-wintering birds such as swan goose (Anser cygnoides) and white-fronted goose (A. albifrons albifrons) [41]. There are several metal mining regions at the side of Poyang Lake, such as Dexing and Yongping Cu mines [42]. The mining activities bring relatively high concentrations of Cu into water and sediment of Poyang Lake [42], which may significantly impact the growth of wetland plants (e.g., Carex).

Figure 1. (a) Location of the study area in Poyang Lake, China and (b) the spatial distribution of 71 Carex samples.

Figure 1. (a) Location of the study area in Poyang Lake, China and (b) the spatial distribution of 71 Carex samples.

2.2. Data Collection

The fieldwork was conducted during April 2013 in Poyang Lake. A total of nine sites (150 × 150 m) were randomly selected (Figure 1b), covering 71 plots (1 × 1 m) with large areas containing Carex communities. Any two plots were at least 30 m apart. At each plot, canopy reflectance measurements (350−2500 nm) were made using an ASD FieldSpec® 3 portable spectroradiometer (Analytical Spectral Devices, Inc., Boulder, CO, USA) with a field of view of 10°. Before each spectral measurement, calibrated reflectance measurements were taken using a white Spectralon panel to minimize the effects of changes in solar irradiance and atmospheric conditions on canopy reflectance. At each plot, 10 successive spectra were measured at the nadir position from 1 m above the canopy, and their mean values were calculated and recorded as the canopy reflectance spectra. After each spectral measurement, a portable chlorophyll meter (SPAD-502, Minolta Camera Co. Ltd., Osaka, Japan) was used to measure the SPAD readings of Carex samples. During each measurement, direct sunlight was avoided by the operator, and a total of 20 green leaves were randomly measured and averaged as the final SPAD value. Afterwards, five subplots (0.25 × 0.25 m) in the four corners and center of each plot were harvested by clipping leaves (5 cm above the ground) and pooled, and the pooled fresh leaves were immediately put into a labeled sample bag and sent to laboratory for their chemical analyses.

Numerous studies have demonstrated the strong correlation between foliar chlorophyll concentration and SPAD-502 chlorophyll readings [43]. In this study, the chlorophyll concentration (unit: mg∙g⁻¹) of each plot was calculated by the following equation developed by Uddling et al. [43]:

$$Y_{Chl}=0.363e^{0.0452x}$$

(1)

Where Y_Chl is chlorophyll concentration and x is SPAD value.

The collected fresh leaves were cleaned using distilled water to remove soil and dead leaves, air-dried at room temperature for 24 h, dried at 70 °C for 24 h in an oven, ground with an agate mortar, and passed through a 65-mesh sieve (0.25 mm). The ground samples were then pre-processed with HNO₃-H₂SO₄-HCLO₄ using the microwave digestion method. The Cu concentrations (unit: mg∙kg⁻¹) were determined with an AA-6601F Flame Atomic Absorption Spectrometry (FFAS) according to the Chinese National Standards GB3838-2002 [44]. To ensure measurement accuracy, certified reference materials and reagent blanks were used during chemical analyses.

2.3. Spectral Pre-Processing

The 71 canopy reflectance spectra (350−2500 nm) were first reduced to 400−1350 nm because of noises at both edges (<399 nm and >2400 nm) and the strong water absorption regions centered at 1400 and 1940 nm. According to the findings reported by Blackburn and Ferwerda [9], first derivative reflectance spectra can be more suitable as input for WT analysis than original reflectance spectra, due to the strengthening of feature peaks and valleys by derivative analysis. The reduced spectra were then subjected to first derivative analysis with the Savitzky-Golay smoothing method to minimize the impact of soil background and multiple scattering of radiation on canopy reflectance spectra [9,10].

3. Methods

3.1. Selection of Mother Wavelet Function for Wavelet Transform

A wavelet

$\psi (\lambda )$

is an oscillating waveform function with an average value of zero (

${{\displaystyle \int }}_{-\infty }^{+\infty }\psi (\lambda )d\lambda =0$

) [33]. Wavelet transform (WT) decomposes a signal

$s(\lambda )$

into dilated (scaled) and continuous WT (CWT)) or dyadic (corresponding to discrete WT (DWT)) scales [33,34]. The wavelet decomposition, thus, yields a series of wavelet coefficients

$C(a,b)$

:

$$C(a,b)={{\displaystyle \int }}_{-\infty }^{+\infty }s(\lambda )\frac{1}{\sqrt{a}}\psi (\frac{\lambda -b}{a})d\lambda$$

(2)

Here, a and b are scale (spectral width) and position parameters, respectively. For CWT,

$a\in R^{+}$

and

$b\in R$

. For DWT,

$a=2^j,b=k{2}^j$

,

$(j,k)\in Z^2$

, and j is the decomposition level.

From the space-saving perspective of wavelet decomposition (Equation (2)), it is computationally expensive for CWT but efficient for DWT. Furthermore, DWT is also sufficient for exact reconstruction to ensure the same dimension as the original signal, and it can preserve general traits and magnify subtle features [39,40,45]. For this reason, DWT was used for hyperspectral signal decomposition and reconstruction, and it was implemented using the Wavelet Toolbox (Version 4.6) of Matlab 2010b (The MathWorks, Inc., Natick, MA, USA).

From the uncertainty perspective of wavelet decomposition (Equation (2)), the wavelet coefficients vary with different mother wavelet functions. There are more than 50 mother wavelet functions used in various studies, and there is no single or generally accepted criterion for choosing an appropriate wavelet function for DWT [9,33,38,40,45]. Among these mother wavelet functions, the Daubechies wavelet (dbN, N is the order) has been widely used for signal analysis, because it can detect the discontinuity in vibration signals and provide compact support and orthogonal wavelets [38,45]. Considering the findings of Liu et al. [31] and Koger et al. [38], db5 was here used as the mother wavelet function, mainly due to its ability in amplifying vegetation stress information. The db5 wavelet is an orthogonal wavelet with the characteristics of compact support, symmetry and smoothness, and its accuracy of signal reconstruction is high with little phase distortion [33,34].

3.2. Spectral Decomposition and Reconstruction Using Discrete Wavelet Transform

The decomposition of DWT was implemented using a dyadic filter tree with down-sampling and filtering (Figure 2). The original signal is passed through a series of high-pass and low-pass filters. The low-pass component provides an approximation of signal, reflecting the general features. The high-pass component provides the detail of signal, reflecting the subtle features. This hierarchical decomposition results in the dyadic decrease of dimension for both approximation and detail coefficients.

Figure 2. Decomposition and reconstruction processes of discrete wavelet transform (DWT) (The figure was adapted based on the original figure in Misiti et al. [33]).

Figure 2. Decomposition and reconstruction processes of discrete wavelet transform (DWT) (The figure was adapted based on the original figure in Misiti et al. [33]).

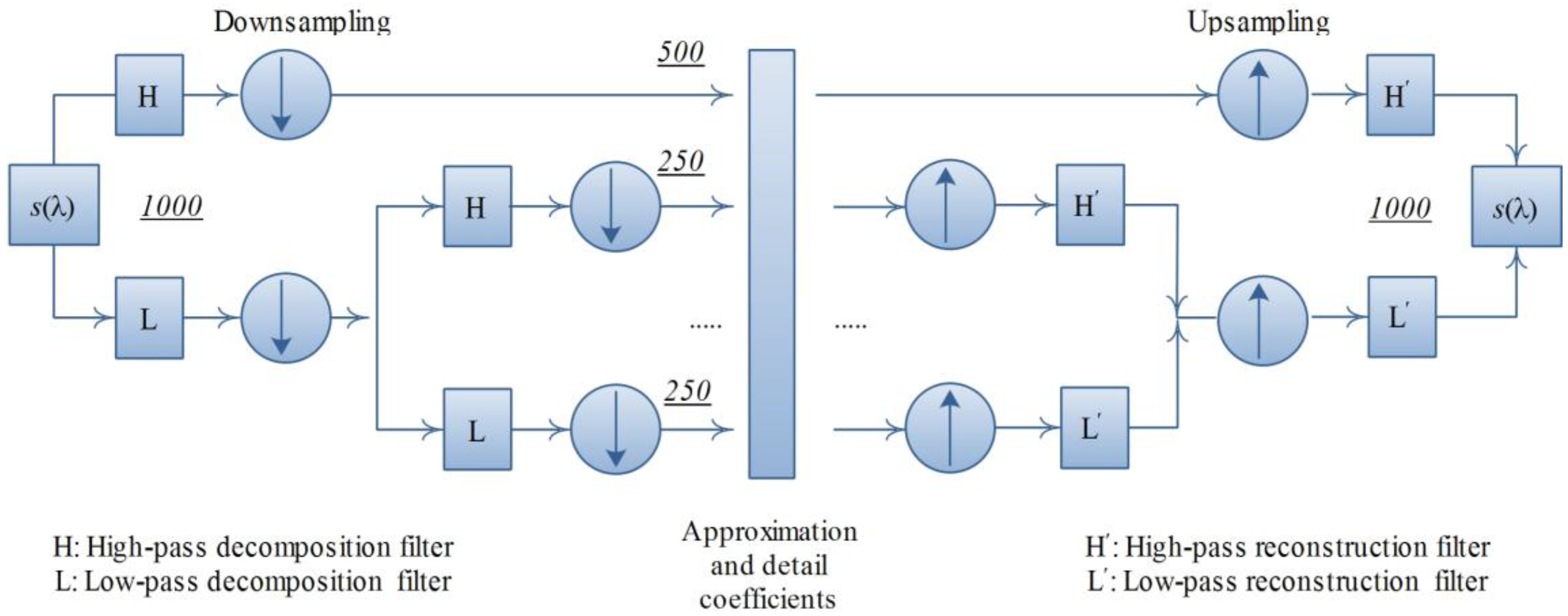
The approximation and detail reflectance can be reconstructed from their coefficient vectors by up-sampling and filtering. The reconstruction process was performed as described by Misiti et al. [33]. This reconstruction provides the same dimension as the original spectral signal, which is beneficial for further spectral analysis [22].

3.3. Defining a Wavelet-Based Area Parameter Using Discrete Wavelet Transform

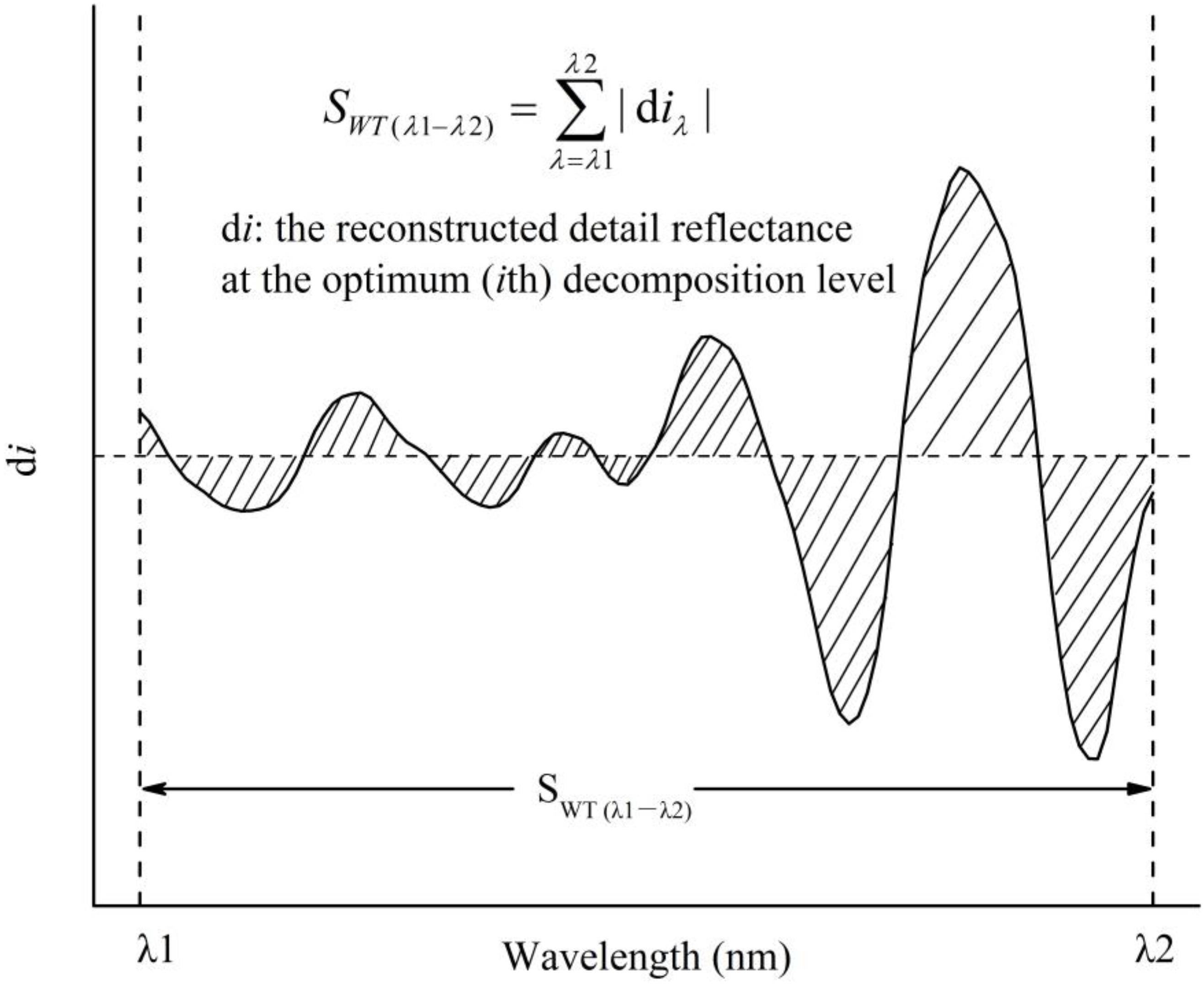
As mentioned in the Introduction, the purpose of this study was to define a wavelet-based area parameter (S_{WT (λ1 − λ2)}) (Figure 3) for estimating Cu concentration in Carex leaves, because WT can magnify subtle spectral signatures of biophysical and biochemical components. Three steps were taken to achieve this goal:

• Selection of the optimal decomposition level for DWT analysis of pre-processed reflectance (i.e., first derivative reflectance);

• Rough identification of the spectral region (λ1 − λ2 nm) sensitive to foliar Cu variations;

• Optimization of the spectral region for the area parameter.

For the first step, two simple rules were proposed:

(1)

The reconstructed approximation reflectance was required to maximize the spectral similarity of first derivative reflectance to ensure the general shape and localization of spectral features;

(2)

The reconstructed detail reflectance required maximizing the correlation with foliar Cu concentrations to magnify the subtle spectral information.

Figure 3. Wavelet-based area parameter S_{WT (λ1 − λ2)} (absolute area).

Figure 3. Wavelet-based area parameter S_{WT (λ1 − λ2)} (absolute area).

The spectral similarity analysis was performed for each sample using Minkowski distance (D_Mink ). The D_Mink between first derivative reflectance (D_λ ) and reconstructed approximation reflectance (A_λ ) for each wavelength λ (400−1350 nm) is given as follows [46]:

$$D_{Mink}=({\displaystyle \sum }_{\lambda =400}^{1350}{(D_{\lambda }-A_{\lambda })}^2{)}^{\frac{1}{2}}$$

(3)

For each sample, D_Mink between D_λ and A_λ at different decomposition levels (a1, a2, a3, a4, a5, a6, a7 and a8) was calculated, respectively. Correlation analysis was implemented using the maximum absolute Pearson's correlation coefficient (r) between Cu concentration and reconstructed detail reflectance at different decomposition levels (d1, d2, d3, d4, d5, d6, d7 and d8).

For the second step, the foliar Cu concentrations of 71 samples were first classified into three groups based on the findings of Kabata-Pendias and Pendias [26]: safe level (0−30 mg∙kg⁻¹), low pollution (30−60 mg∙kg⁻¹), and moderate pollution (60−120 mg∙kg⁻¹). For each group, the mean reconstructed detail reflectance at the optimum decomposition level was calculated and plotted, respectively. The sensitive spectral region (λ1 − λ2 nm) was roughly determined by observing whether the amplitudes of mean reflectance accorded with the increasing mean Cu concentrations for the three groups.

For the third step, the appropriate spectral region was optimized by calculating the Pearson's correlation coefficient (r) between foliar Cu concentrations and S_{WT (λ1−λ2)} with different adjacent spectral regions. Specifically, λ1 first remained unchanged while λ2 was changed into λ2 + k × 5 (k = 1, 2, …, 10), and then λ2 remained unchanged while λ1 was changed into λ1 − k × 5 (k = 1, 2, …, 10), respectively. The area parameter with the maximum r against foliar Cu concentration was considered as the optimum area parameter, which was further used for foliar Cu estimation.

3.4. Estimation of Foliar Cu Concentration Using the Wavelet-Based Area Parameter

For reliable quantification of foliar Cu concentration, the dataset (Cu concentration and S_{WT (λ1 − λ2)}, N = 71) was randomly split into calibration set (N = 36) and validation set (N = 35) by 1000 times, resulting in 1000 different calibration and validation sets. Each of the 1000 linear calibration models (

$Y=k\times S_{WT(\lambda 1-\lambda 2)}+b$

) was calibrated with the calibration set, and then independently validated with the corresponding validation set. The root mean square error of calibration (RMSE_Cal) and validation (RMSE_Val), the determination coefficient of calibration (R² _Cal) and validation (R² _Val) and residual prediction deviation (RPD, the ratio of standard deviation to RMSE_Val) values were calculated to evaluate the performance of each model. The R² _Val and RPD values indicate the quality and predictive power of the calibration n models, respectively. The statistics of model equation parameters (k and b), RMSE_Cal, R² _Cal, RMSE_Val, R² _Val, and RPD values for the 1000 models were reported.

In order to explore the ability of S_{WT (λ1−λ2)} in estimating Cu concentrations, the general calibration model using the mean k and b values was employed with the full dataset (N = 71), and measured against the predicted values, which were then plotted. Moreover, the mean absolute relative error (MARE = (∑|predicted value − measured value|/measured value)/N) was calculated for the three concentration groups (safe level, low pollution, and moderate pollution), respectively.

3.5. Performance Comparison between the Wavelet-Based Area Parameter and Published Spectral Parameters

In order to check the practicality of the wavelet-based area parameter (S_{WT (605−720)}), its performance was compared to that of ten classical chlorophyll-related spectral parameters (Table 1 [11,13,14,16,17,18,19,20,30,47]) and one published wavelet-based spectral parameter (FDWT_480−850, the fractal dimension of reflectance with wavelet transform using detail reflectance at the fifth decomposition level in the region of 480−850 nm) [22] using the bootstrapping method with 1000 replicates. Bootstrapping provided the estimates of statistics (mean and confidence intervals) for the determination coefficient (R²) for estimating foliar Cu concentrations with the 12 spectral parameters (including S_{WT (605−720)}) using the full dataset (N = 71). In addition, one-way ANOVA (analysis of variance) using the least squares difference (LSD) method was performed to determine whether there were significant differences in the mean R² between S_{WT (605−720)} and the aforementioned 11 chlorophyll-related and wavelet-based spectral parameters.

Table 1. Some classical chlorophyll-related spectral parameters. ^a

Table 1. Some classical chlorophyll-related spectral parameters. ^a

Spectral Parameter	Formula	Reference
Modified simple ratio (MSR [670, 800])	$\frac{({\rho }_{800}/{\rho }_{670})-1}{\sqrt{({\rho }_{800}/{\rho }_{670})+1}}$	Chen [17]
Modified simple ratio (MSR [500, 720])	$\frac{{\rho }_{720}^{\prime }-{\rho }_{500}^{\prime }}{{\rho }_{700}^{\prime }-{\rho }_{500}^{\prime }}$	Le Maire et al. [13]
Normalized difference (ND [710, 925]	$\frac{{\rho }_{925}-{\rho }_{710}}{{\rho }_{925}+{\rho }_{710}}$	Le Maire et al. [19]
Modified normalized difference (MND [445, 750])	$\frac{{\rho }_{750}-{\rho }_{705}}{{\rho }_{750}+{\rho }_{705}-2{\rho }_{445}}$	Sims and Gamon [16]
Modified Chlorophyll absorption ratio index (MCARI [670, 700])	$[({\rho }_{700}-{\rho }_{670})-0.2\times ({\rho }_{700}-{\rho }_{550})](\frac{{\rho }_{700}}{{\rho }_{670}})$	Daughtry et al. [11]
Optimized soil-adjusted vegetation index (OSAVI [670, 800])	$\frac{(1+0.16)({\rho }_{800}-{\rho }_{670})}{{\rho }_{800}+{\rho }_{670}+0.16}$	Rondeaux et al. [47]
MCARI/OSAVI [705, 750]	$\frac{[({\rho }_{750}-{\rho }_{705})-0.2\times ({\rho }_{750}-{\rho }_{550})]({\rho }_{750}/{\rho }_{705})}{(1+0.16)({\rho }_{750}-{\rho }_{705})/({\rho }_{750}+{\rho }_{705}+0.16)}$	Wu et al. [14]
Red edge position (REP)	$-(c_1-c_2)/(m_1-m_2)$	Cho and Skidmore [20]
Red edge area (SRE)	${\displaystyle \sum _{\lambda =680}^{780}}{\rho }_{\lambda }^{\prime }$	Filella et al. [30]
Normalized area over reflectance curve (NAOC [643, 795])	$1-\frac{{{\displaystyle \int }}_{643}^{795}{\rho }_{\lambda }d\lambda }{{\rho }_{max}(795-643)}$	Delegido et al. [18]

4. Results

4.1. Relationship between Foliar Cu and Chlorophyll Concentration

The foliar Cu concentrations (N = 71) ranged from 6.58 to 107.71 mg∙kg⁻¹ with a mean value of 41.36 mg∙kg⁻¹, and the chlorophyll concentrations calculated by SPAD-502 chlorophyll readings ranged from 0.81 to 2.00 g∙kg⁻¹ with a mean value of 1.36 g∙kg⁻¹. Based on the concentrations of Cu, the 71 samples could be classified into three groups: safe level (0−30 mg∙kg⁻¹, N = 40, mean = 14.46 mg∙kg⁻¹), low pollution (30−60 mg∙kg⁻¹, N = 16, mean = 53.30 mg∙kg⁻¹), and moderate pollution (60−120 mg∙kg⁻¹, N = 15, mean = 100.33 mg∙kg⁻¹). The mean chlorophyll concentrations of the three groups were 1.51, 1.32 and 1.01 g∙kg⁻¹, respectively. Figure 4 shows that the Cu concentration was negatively and strongly correlated with the chlorophyll concentration (r = −0.719, p < 0.001).

Figure 4. Relationship between foliar Cu and chlorophyll concentration (N = 71).

Figure 4. Relationship between foliar Cu and chlorophyll concentration (N = 71).

4.2. Extraction of the Wavelet-Based Area Parameter from Canopy Reflectance Spectra

Figure 5 illustrates the reconstructed approximation and detail reflectance (400−1350 nm) with eight different decomposition levels using the DWT method. Evidently, the derivative reflectance (Figure 5b) strengthened the spectral differences of original reflectance (Figure 5a). The reconstructed approximation reflectance preserved the spectral features (e.g., around 600 nm) of derivative reflectance from the first to fourth decomposition level (Figure 5c−f); and the reconstructed detail reflectance magnified the subtle features (e.g., around 700 nm) at the third and fourth decomposition level (e.g., Figure 5m,n).

The higher decomposition level resulted in the coarser spectral resolution and the greater loss of spectral information (e.g., Figure 5i,j), while the lower decomposition level might have more noise for reconstructed detail reflectance (e.g., Figure 5k,l).

The order of Minkowski distance (D_Mink ) was a1 < a2 < a3 < a4 < a5 < a6 < a7 < a8 (Figure 6a), suggesting that the reconstructed approximation reflectance at the first to fourth decomposition level were more similar to derivative reflectance than those at the fifth to eighth decomposition level. The reconstructed detail reflectance at the fourth decomposition level (d4) showed the most pronounced relationship with foliar Cu concentration (Figure 6b) among the eight decomposition levels.

Given the above results, the optimal decomposition level was chosen at the fourth level, because this level met the two proposed rules described in Section 3.3. The d4 reflectance was then used for further area parameter extraction to magnify the subtle spectral information sensitive to Cu variation.

Figure 5. One example (Sample 1) of plots of original reflectance (a), derivative reflectance (b), reconstructed approximation reflectance at the first to eighth decomposition level (c−j) and reconstructed detail reflectance at the first to eighth decomposition level (k−r) using discrete wavelet transform (db5 was the mother wavelet function).

Figure 5. One example (Sample 1) of plots of original reflectance (a), derivative reflectance (b), reconstructed approximation reflectance at the first to eighth decomposition level (c−j) and reconstructed detail reflectance at the first to eighth decomposition level (k−r) using discrete wavelet transform (db5 was the mother wavelet function).

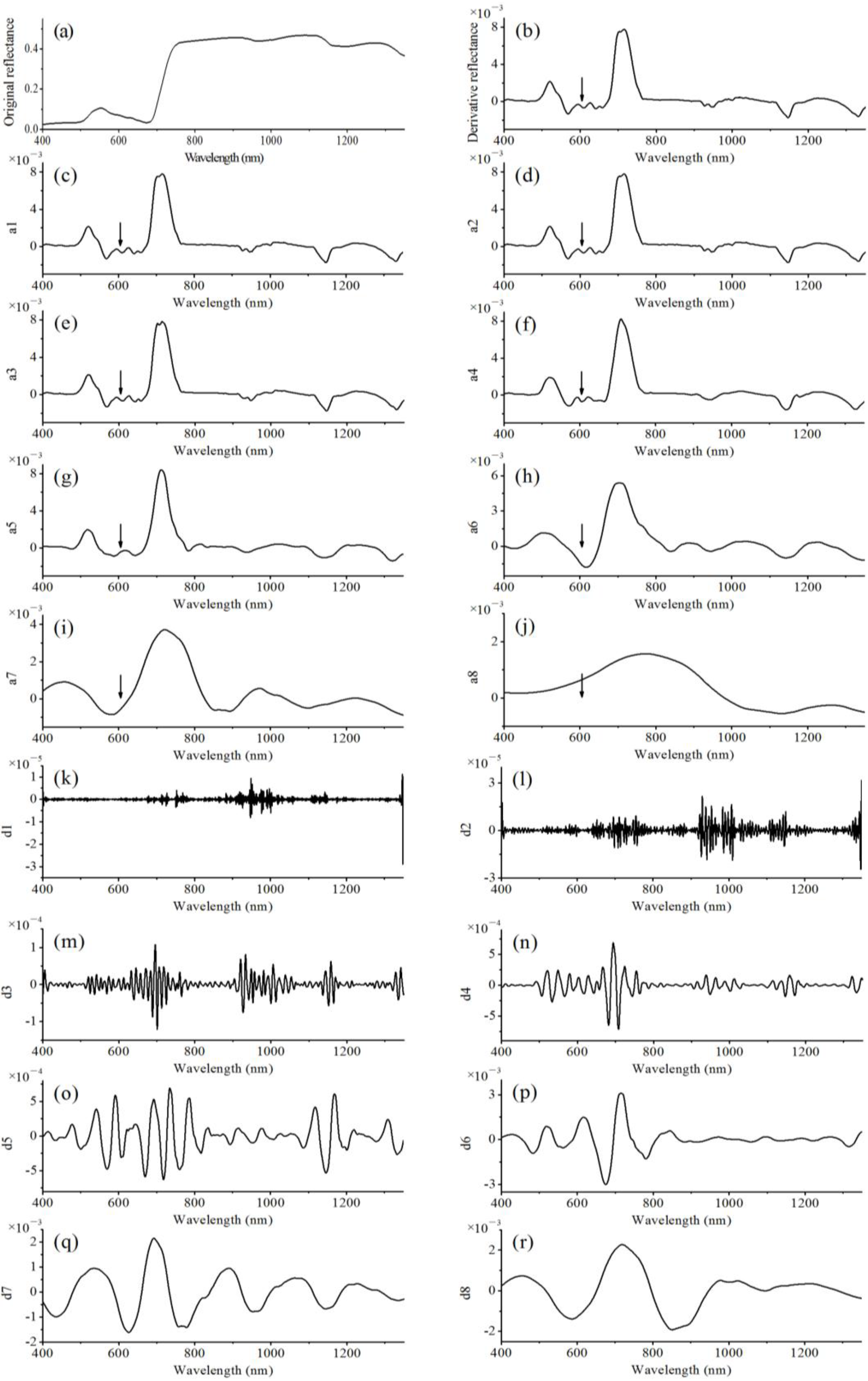
Figure 6. (a) The Minkowski distance between derivative reflectance and reconstructed approximation reflectance (a1, a2, a3, a4, a5, a6, a7 and a8) at different decomposition levels for each sample (N = 71) and (b) the maximum absolute Pearson's correlation coefficient (r) between foliar Cu concentration and reconstructed detail reflectance (d1, d2, d3, d4, d5, d6, d7 and d8) at different decomposition levels.

Figure 6. (a) The Minkowski distance between derivative reflectance and reconstructed approximation reflectance (a1, a2, a3, a4, a5, a6, a7 and a8) at different decomposition levels for each sample (N = 71) and (b) the maximum absolute Pearson's correlation coefficient (r) between foliar Cu concentration and reconstructed detail reflectance (d1, d2, d3, d4, d5, d6, d7 and d8) at different decomposition levels.

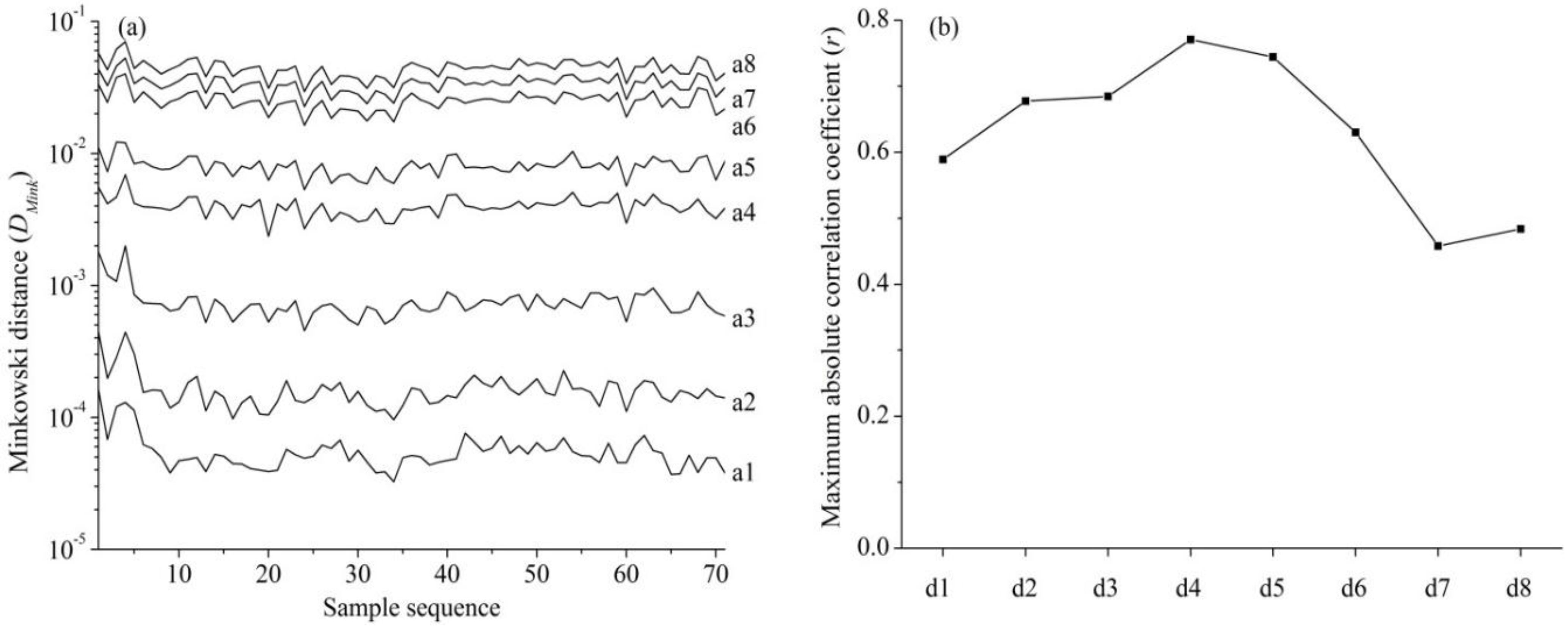
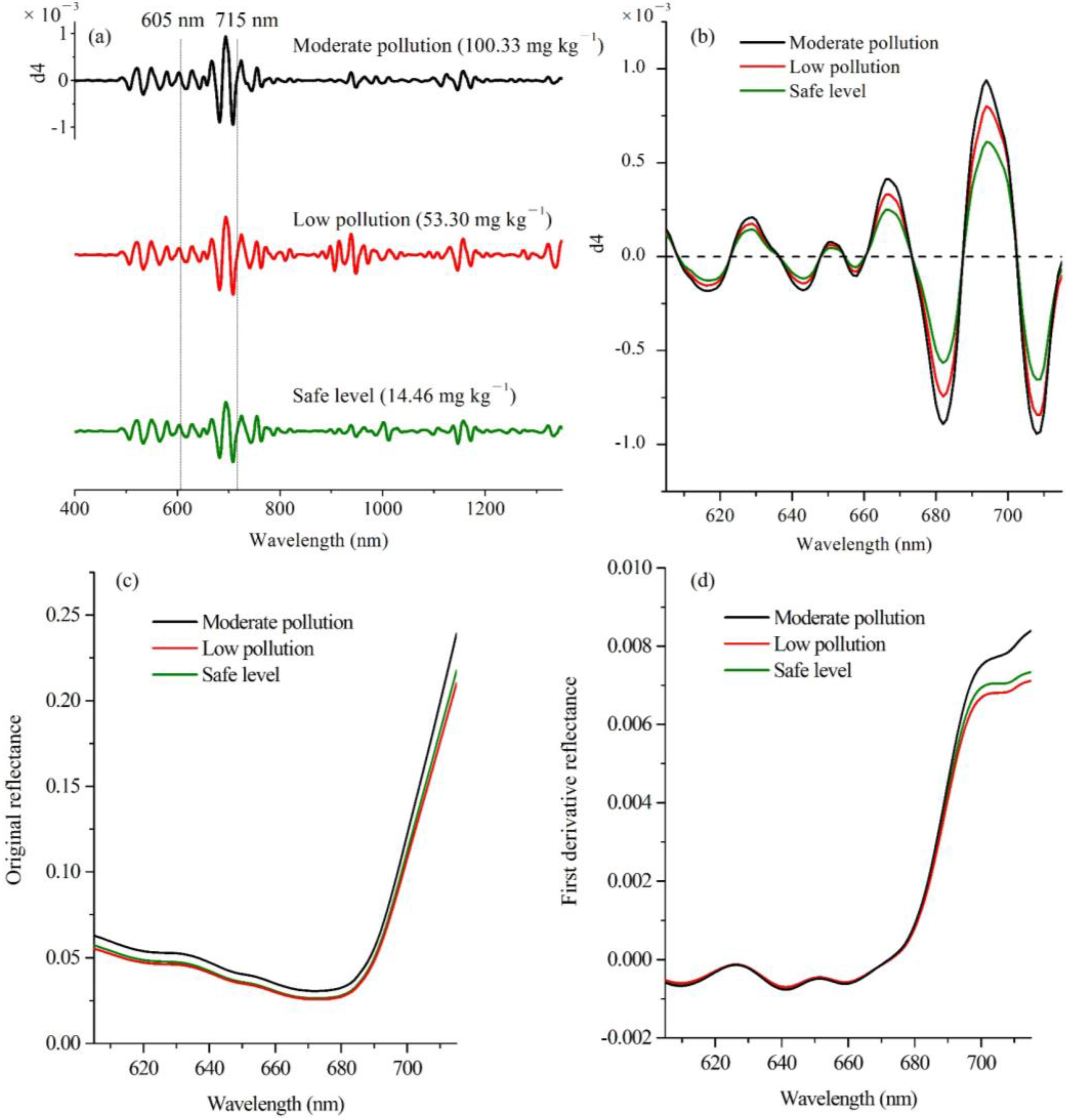
Figure 7a,b demonstrated that the samples with the higher Cu concentrations tended to have stronger d4 reflectance over 605−715 nm, while the d4 reflectance over the other continuous spectral regions did not exhibit such close relationship with Cu concentration. In contrast, the mean original (Figure 7c) and first derivative reflectance spectra (Figure 7d) over 605−715 nm did not have evident peaks and valleys that existed for d4 reflectance spectra to enhance the potential subtle spectral features, and their reflectance values did not show a good relationship with Cu concentrations because their reflectance values in the low pollution group and safe level group were similar and hardly distinguished.

Table 2. Pearson's correlation coefficient (r) between foliar Cu concentrations and S_{WT (λ1−λ2)} with different spectral regions.

Table 2. Pearson's correlation coefficient (r) between foliar Cu concentrations and S_{WT (λ1−λ2)} with different spectral regions.

λ1 (nm)	λ2 (nm)	r	λ1 (nm)	λ2 (nm)	r
605	715	0.836	605	715	0.836
	720	0.838	600		0.832
	725	0.835	595		0.816
	730	0.832	590		0.805
	735	0.831	585		0.794
	740	0.827	580		0.782
	745	0.815	575		0.779
	750	0.807	570		0.758
	755	0.791	565		0.723
	760	0.778	560		0.720
	765	0.762	555		0.718

To determine the precise spectral region, the rough spectral region (605−715 nm) was slightly tuned with different adjacent spectral regions, and the Pearson's correlation coefficients (r) between the corresponding area parameters and Cu concentrations (N = 71) were calculated, respectively (Table 2). Results showed that the spectral region over 605−720 nm was optimal, because S_{WT (605−720)} had the strongest correlation (r = 0.838, p < 0.001) with Cu concentration. The area parameter S_{WT (605−720)} (range = 0.0113−0.0341, mean = 0.0233, N = 71) was then used for further analysis.

Figure 7. (a) The mean d4 reflectance (400−1350 nm), (b) the amplifying d4 reflectance (605−715 nm), (c) the mean original reflectance (605−715 nm), (d) the mean first derivative reflectance (605−715 nm) for the samples in the group of safe level (0−30 mg∙kg⁻¹), low pollution (30−60 mg∙kg⁻¹), and moderate pollution (60−120 mg∙kg⁻¹), respectively.

Figure 7. (a) The mean d4 reflectance (400−1350 nm), (b) the amplifying d4 reflectance (605−715 nm), (c) the mean original reflectance (605−715 nm), (d) the mean first derivative reflectance (605−715 nm) for the samples in the group of safe level (0−30 mg∙kg⁻¹), low pollution (30−60 mg∙kg⁻¹), and moderate pollution (60−120 mg∙kg⁻¹), respectively.

4.3. Foliar Cu Estimation with the Wavelet-Based Area Parameter

A total of 1000 linear calibration models were established with 1000 calibration sets (N = 36) for estimating foliar Cu concentrations with the wavelet-based area parameter (S_{WT (605−720)}), and they were independently validated with the corresponding validation sets (N = 35) (Table 3). Evidently, the calibration and validation results varied greatly with different dataset partitioning experiments. The general model using the mean k and b values (

$Y_{Cu}=7098.05\times S_{WT(605-720)}-129.12$

) could reflect the general and unbiased relationship between Cu concentration and S_{WT (605−720)}. The 1000 calibration models reported a mean R² _Val value of 0.710 and RPD value of 1.75.

Table 3. Calibration and validation results of estimating foliar Cu concentration based on 1000 random dataset partitioning experiments.

Table 3. Calibration and validation results of estimating foliar Cu concentration based on 1000 random dataset partitioning experiments.

Statistics	$Y_{Cu}=k{S}_{WT(605-720)}+b$		Calibration (N = 36)		Validation (N = 35)
	k	b	RMSECal (mg∙kg−1)	R2 Cal	RMSEVal (mg∙kg−1)	R2 Val	RPD
Minimum	5176.71	－193.28	11.82	0.491**	14.49	0.516**	1.16
Maximum	9800.62	－89.55	22.67	0.885**	26.91	0.822**	2.24
Mean	7098.05	－129.12	18.37	0.710**	20.16	0.706**	1.75

Figure 8. Scatterplot of the measured against predicted Cu concentration with the full dataset (N = 71) based on the general model (

$Y_{Cu}=7098.05\times S_{WT(605-720)}-129.12$

) for Cu estimation.

Figure 8. Scatterplot of the measured against predicted Cu concentration with the full dataset (N = 71) based on the general model (

$Y_{Cu}=7098.05\times S_{WT(605-720)}-129.12$

) for Cu estimation.

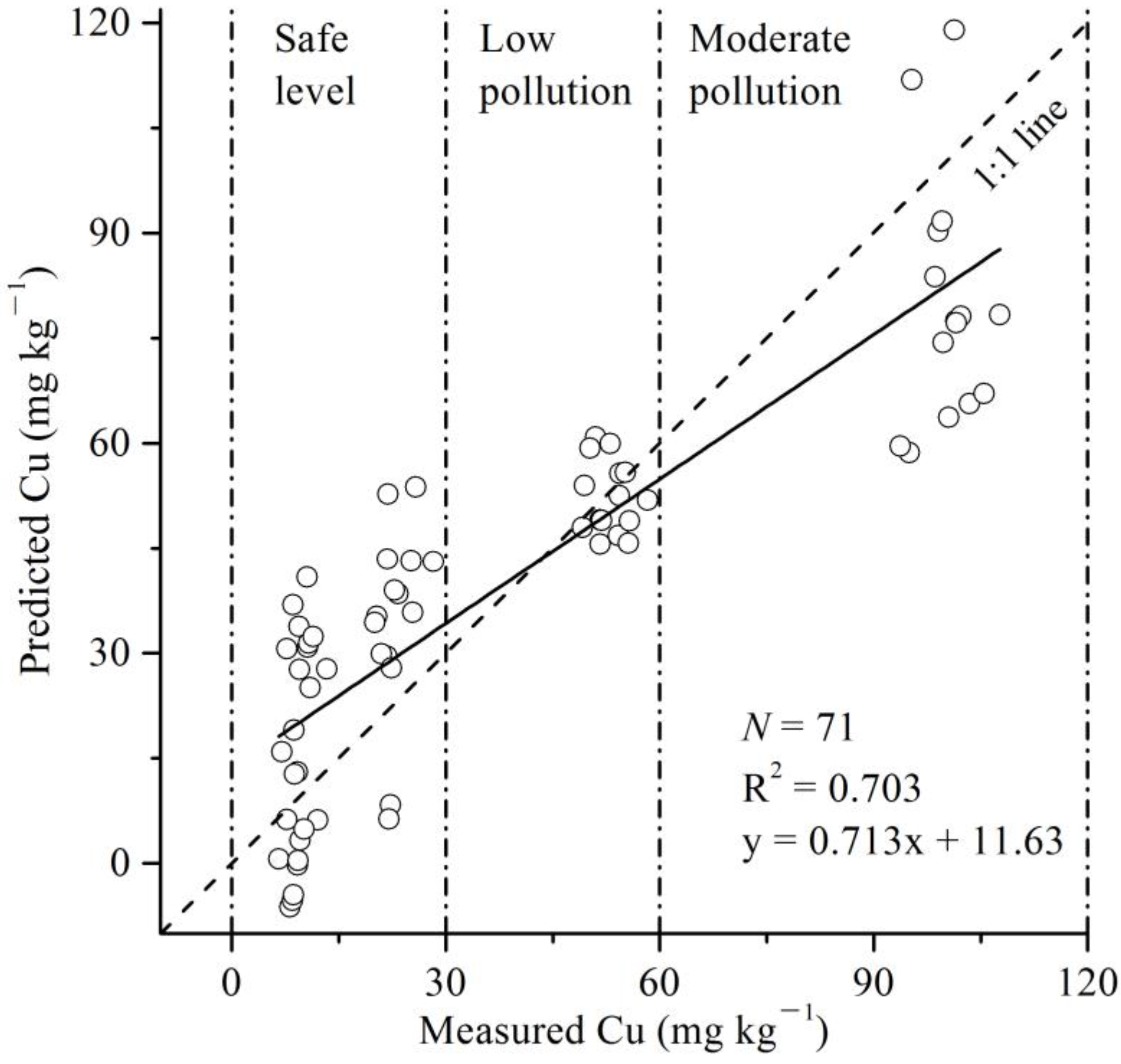
The scatterplot illustrates the agreement between the measured and predicted Cu concentrations using the general model (N = 71) (Figure 8). The sample points in the low pollution group (30−60 mg∙kg⁻¹) were closer to 1:1 line than the other two groups. The mean absolute relative error (MARE) between predicted and measured values was 63.07%, 9.82% and 34.86% for the safe level, low pollution, and moderate pollution groups, respectively. This indicates that more reliable and accurate prediction of foliar Cu concentrations can be performed at the concentration range of 30−60 mg∙kg⁻¹.

4.4. Performance Comparison between the Wavelet-Based Area Parameter and Published Spectral Parameters

The performance of the wavelet-based area parameter (S_{WT (605−720)}) was compared to that of ten classical chlorophyll-related spectral parameters and one published wavelet-based spectral parameter (FDWT_480−850) for quantifying foliar Cu concentration (N = 71) (Table 4). The bootstrapping results showed that S_{WT (605−720)} provided the highest mean determination coefficient for quantifying Cu concentration (R² = 0.706, p < 0.001) among these parameters. The ANOVA test results showed there to be significant difference (p < 0.05) between S_{WT (605−715)} and each of the 11 published spectral parameters in the mean R² values for foliar Cu quantification.

Table 4. Bootstrapped determination coefficient (R²) for quantifying foliar Cu concentration with the 10 classical chlorophyll-related spectral parameters listed in Table 1 and one published wavelet-based area parameter using the full dataset (N = 71).

Table 4. Bootstrapped determination coefficient (R²) for quantifying foliar Cu concentration with the 10 classical chlorophyll-related spectral parameters listed in Table 1 and one published wavelet-based area parameter using the full dataset (N = 71).

Spectral Parameter	Mean	LCL 95%	UCL 95%
MSR [670, 800]	0.087	0.001	0.218
MSR [500, 720]	0.192**	0.040	0.315
ND [710, 925]	0.193**	0.058	0.336
MND [445, 750]	0.187**	0.055	0.312
MCARI [670, 700]	0.515**	0.394	0.614
OSAVI [670, 800]	0.168**	0.021	0.327
MCARI/OSAVI [705, 750]	0.039	0.010	0.157
REP	0.178**	0.038	0.305
SRE	0.214**	0.046	0.393
NAOC [643, 795]	0.136*	0.027	0.262
FDWT480−850	0.145*	0.107	0.276
SWT (605−720) (this paper)	0.706**	0.570	0.773

Despite S_RE, NAOC [643, 795], and S_{WT (605−720)} are area parameters with the same spectral region (680−720 nm), S_RE and NAOC [643, 795] showed much poorer correlations with foliar Cu concentrations than S_{WT (605−720)}. This indicates that the spectral information over 605−720 nm was more sensitive to Cu variations than that over the red edge region (680−780 nm) and 643−795 nm. Both of FDWT_480−850 and S_{WT (605−720)} are wavelet-based spectral parameters, but FDWT_480−850 exhibited much poorer performance than S_{WT (605−720)}.

Among the 10 classical chlorophyll-related spectral parameters, MCARI [670, 700] had the closest correlation with Cu concentration (R² = 0.515, p < 0.001), while the other nine parameters showed much poorer correlations, indicating that these parameters were not sensitive enough to effectively extract Cu concentration information. In addition, the mean red edge position (REP) for safe level (0−30 mg∙kg⁻¹), low pollution (30−60 mg∙kg⁻¹), and moderate pollution groups (60−120 mg∙kg⁻¹) of Cu concentrations was 709.78, 707.65 and 707.53 nm, respectively. This suggests that the REP tends to move to the shorter wavelengths as the concentration of Cu increases.

5. Discussion

This study is the first attempt to develop a wavelet-based area parameter (S_{WT (605−720)}) from canopy reflectance to enhance the subtle spectral changes related to foliar chlorophyll concentration under Cu stress, and use it to indirectly estimate Cu concentration in Carex leaves. According to the interpretation of R2 value given by Williams [48] and RPD value given by Saeys et al. [49], the general model (

$Y_{Cu}=7098.05\times S_{WT(605-720)}-129.12$

) using the mean k and b values of the 1000 models (Table 3) demonstrated capable of distinguishing between high and low values of foliar Cu concentrations (0.66 < R² _Val < 0.81,1.5 < RPD < 2.0). The main mechanism of such successful estimation originates from the strong correlation between Cu and chlorophyll (Figure 4). Despite the element of Cu in plant leaves does not have evident absorption features, the high Cu concentration might trigger the decrease of foliar chlorophyll concentration, which can change the leaf reflectance spectrum [4,23,25,29]. This can be interpreted by that: the high concentration of Cu can stimulate the formation of free radicals and reduce the number of pores among mesophyll cells [1,3]; and chlorophyll concentration is a main influencing factor on leaf and canopy spectral characteristics in the visible region [16,47]. Hence, our study employed the coupling of wavelet transform and area parameters to capture the potential spectral changes related to chlorophyll under Cu stress for the accurate estimation of foliar Cu concentration. To some extent, the spectral region of 605−720 nm was the sensitive region reflecting such subtle spectral changes. The region of 605−680 nm is the strong absorption region of chlorophyll [8,11], and the region of 680−720 nm is part of the red edge region (680−720 nm), which has been found to be closely related to foliar chlorophyll concentration [12,16,23,24].

The general model involved more accurate predictions at the low pollution level than that at the safe level for the estimation of Cu concentrations (Figure 8), indicating that S_{WT (605−720)} had the potential to detect low levels of Cu pollution in Carex leaves. Several studies have attempted to use shifts in the REP to detect heavy metal pollution in plant leaves, because REP is sensitive to metal-polluted leaves [23]. The current study and a previous report of Liu et al. [22] both showed there to be a blue shift in the REP as concentrations of Cu increased in plant leaves. However, both studies reported a very low relationship between REP and foliar Cu concentrations. This might be because the Cu concentrations in plant leaves were not high enough to significantly affect the reflectance amplitude in the near-infrared waveband.

Published studies have reported R² _Val values of 0.740−0.967 for foliar Cu estimation with hyperspectral remote sensing techniques [21,22,23]. The current study obtained R² _Val values of 0.516−0.822 with a mean value of 0.706 for foliar Cu estimation (Table 3) based on 1000 random dataset partitioning experiments. The relatively low prediction results for Cu estimation in this study might be due to the narrow range of Cu concentrations (6.58−107.71 mg∙kg⁻¹) within the leaf samples collected in natural wetlands, compared with that in other studies. For example, Liu et al. [21] provided Cu concentrations with 60−576 mg∙kg⁻¹ within leaf samples collected along a Cu-polluted river. An unrelated Liu et al. [23] reported Cu concentrations with 18.12−502.05 mg∙kg⁻¹ within leaf samples cultivated in the laboratory using soils with artificially-controlled Cu concentrations.

The bootstrapping (Table 4) and ANOVA test results demonstrated the statistically significant superiority of S_{WT (605−720)} over the classical chlorophyll-related and published wavelet-based spectral parameters for estimating Cu concentration in Carex leaves. One possible reason for this may be that the chlorophyll-related spectral parameters were directly correlated with foliar chlorophyll content and were indirectly related to Cu concentrations, which rendered the correlations less closely. Secondly, the published spectral parameters and wavelet coefficients may be sensitive to background effects, plant species, study areas, or vegetative stages, possibly rendering predictions of biochemical or biophysical parameters of plants inconsistent and causing these spectral parameters not generalized in different environment conditions [12,14,16,22,47]. Noticeably, MCARI [670, 700] behaved much better than the other nine chlorophyll-related spectral parameters. It is hard to interpret this outperformance; the main reason may be that both of 670 and 700 nm might be sensitive to chlorophyll variation as well as to Cu variation in plant leaves.

The estimation results further demonstrate the successful application of WT in heavy metal estimation in plant leaves, because WT could preserve the general spectral features and location, as well as magnify subtle spectral changes (Figure 5). Many studies also have made good use of this advantage in different fields of remote sensing, and they obtained good accuracies of classification or estimation [9,22,38,39]. However, the evident disadvantage of WT is that there is still no single universal methodology for choosing the optimal mother wavelet function and decomposition level of signal [45]. For this reason, such selection is normally determined by complicated optimization calculation or prior knowledge. For example, Koger et al. [38] investigated 36 different mother wavelets to determine the effect of mother wavelet selection on the ability to detect the presence of pitted morning-glory, demonstrating that Daubechies wavelet (db3 and db5) and Coiflets wavelet (coif5) were the best mother wavelets; Pu and Gong [39] and Liu et al. [22] directly chose db3 at the eighth decomposition level and db5 at the fifth decomposition level based on prior knowledge, respectively. In contrast, the present study combined prior knowledge with simple optimization calculation (i.e., spectral similarity analysis and correlation analysis) in choosing the optimum mother wavelet function and decomposition level to avoid time-consuming experiments and obtain reliable results.

In this study, the optimum decomposition level for WT analysis of canopy hyperspectral data was four (or scale 2⁴ = 16), suggesting that the original signal (400−1350 nm) was decomposed into several wavelet coefficients with a spectral interval of 16 nm. Among the hyperspectral sensors used frequently, HyMap offers a similar bandwidth (15−16 nm) in the visible and near-infrared waveband (450−890 nm). It may be helpful to extend the wavelet-based area parameter S_{WT (605−720)} from canopy reflectance to HyMap image reflectance, which may make it possible to monitor Cu concentrations in Carex leaves at the landscape scale and improve the early warning of Cu pollution in Carex-dominated wetland ecosystem.

Admittedly, the applicability of the proposed wavelet-based area parameter for foliar Cu estimation to the other situations might be limited due to the differences of species, vegetative stages, and biological and environmental conditions, which is a tough issue for statistical modeling methods in retrieving biochemical or biophysical parameters of plants. However, the method presented in this pilot study may be used to estimate the concentrations of other heavy metals. Further, the remotely-sensed estimation of heavy metal concentrations at the canopy or landscape level is still promising for decision-makers and farmers to rapidly understand the growth and metal-pollution condition of plants without intense sampling and chemical analyses.

6. Conclusions

In order to enhance the subtle spectral changes related to foliar chlorophyll concentration under Cu stress, this study attempted to develop a wavelet-based area parameter (S_{WT (605−720)}) from canopy hyperspectral reflectance to estimate Cu concentration in Carex leaves. The main conclusions that can be drawn from the present study are:

(1)

The wavelet-based area parameter could be used to indirectly estimate foliar Cu concentration through the strong correlation between Cu and chlorophyll;

(2)

The wavelet-based area parameter has the potential ability of detecting low concentrations of Cu pollution in Carex leaves;

(3)

The wavelet-based area parameter was superior to published chlorophyll-related and wavelet-based spectral parameters for estimating Cu concentration in Carex leaves.

Despite the abovementioned advantages of the wavelet-based area parameter technique, further research is needed to test its transferability and robustness for estimating Cu concentrations on other plant species in different biological and environmental conditions.

Acknowledgments

This study was supported by the National Natural Science Foundation of China (Grant No. 41171290). The authors would like to thank all the anonymous reviewers and the associate editor for their constructive comments and suggestions on this manuscript.

Author Contributions

Junjie Wang analyzed the data, reviewed the literature and prepared the manuscript. Tiezhu Shi took part in the fieldwork. Guofeng Wu, Tiejun Wang and Andrew K. Skidmore developed the research plan. All authors contributed equally to the editing of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

1. Hall, J. Cellular mechanisms for heavy metal detoxification and tolerance. J. Exp. Bot. 2002, 53, 1–11. [Google Scholar] [CrossRef] [PubMed]
2. Dietz, K.J.; Baier, M.; Krämer, U. Free radicals and reactive oxygen species as mediators of heavy metal toxicity in plants. In Heavy Metal Stress in Plants; Prasad, M.N.V., Hagemeyer, J., Eds.; Springer: Berlin, Germany, 1999; pp. 73–97. [Google Scholar]
3. Krause, G.H.; Kaiser, H. Plant response to heavy metals and sulphur dioxide. Environ. Pollut. 1977, 12, 63–71. [Google Scholar] [CrossRef]
4. Macinnis-Ng, C.M.; Ralph, P.J. Towards a more ecologically relevant assessment of the impact of heavy metals on the photosynthesis of the seagrass, Zostera capricorni. Mar. Pollut. Bull. 2002, 45, 100–106. [Google Scholar] [CrossRef]
5. Markert, B. Plants as Biomonitors: Indicators for Heavy Metals in the Terrestrial Environment; VCH Publishers Ltd.: Cambridge, UK, 1993. [Google Scholar]
6. Kooistra, L.; Salas, E.; Clevers, J.; Wehrens, R.; Leuven, R.; Nienhuis, P.; Buydens, L. Exploring field vegetation reflectance as an indicator of soil contamination in river floodplains. Environ. Pollut. 2004, 127, 281–290. [Google Scholar] [CrossRef]
7. Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
8. Curran, P.J.; Dungan, J.L.; Peterson, D.L. Estimating the foliar biochemical concentration of leaves with reflectance spectrometry: Testing the Kokaly and Clark methodologies. Remote Sens. Environ. 2001, 76, 349–359. [Google Scholar] [CrossRef]
9. Blackburn, G.A.; Ferwerda, J.G. Retrieval of chlorophyll concentration from leaf reflectance spectra using wavelet analysis. Remote Sens. Environ. 2008, 112, 1614–1632. [Google Scholar] [CrossRef]
10. Abdel-Rahman, E.M.; Ahmed, F.B.; van den Berg, M. Estimation of sugarcane leaf nitrogen concentration using in situ spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S52–S57. [Google Scholar] [CrossRef]
11. Daughtry, C.; Walthall, C.; Kim, M.; De Colstoun, E.B.; McMurtrey, J., III. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
12. Gitelson, A.A.; Keydan, G.P.; Merzlyak, M.N. Three-band model for noninvasive estimation of chlorophyll, carotenoids, and anthocyanin contents in higher plant leaves. Geophys. Res. Lett. 2006, 33, L11402. [Google Scholar] [CrossRef]
13. Le Maire, G.; Francois, C.; Dufrene, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
14. Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
15. Cheng, T.; Rivard, B.; Sanchez-Azofeifa, A. Spectroscopic determination of leaf water content using continuous wavelet analysis. Remote Sens. Environ. 2011, 115, 659–670. [Google Scholar] [CrossRef]
16. Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
17. Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
18. Delegido, J.; Alonso, L.; González, G.; Moreno, J. Estimating chlorophyll content of crops from hyperspectral data using a normalized area over reflectance curve (NAOC). Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 165–174. [Google Scholar] [CrossRef]
19. Le Maire, G.; François, C.; Soudani, K.; Berveiller, D.; Pontailler, J.-Y.; Bréda, N.; Genet, H.; Davi, H.; Dufrêne, E. Calibration and validation of hyperspectral indices for the estimation of broadleaved forest leaf chlorophyll content, leaf mass per area, leaf area index and leaf canopy biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
20. Cho, M.A.; Skidmore, A.K. A new technique for extracting the red edge position from hyperspectral data: The linear extrapolation method. Remote Sens. Environ. 2006, 101, 181–193. [Google Scholar] [CrossRef]
21. Liu, Y.; Chen, H.; Wu, G.; Wu, X. Feasibility of estimating heavy metal concentrations in Phragmites australis using laboratory-based hyperspectral data—A case study along Le'an River, China. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S166–S170. [Google Scholar] [CrossRef]
22. Liu, M.; Liu, X.; Ding, W.; Wu, L. Monitoring stress levels on rice with heavy metal pollution from hyperspectral reflectance data using wavelet-fractal analysis. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 246–255. [Google Scholar] [CrossRef]
23. Liu, S.; Liu, X.; Hou, J.; Chi, G.; Cui, B. Study on the spectral response of Brassica campestris L. leaf to the copper pollution. Sci. China Ser. E-Tech. Sci. 2008, 51, 202–208. [Google Scholar] [CrossRef]
24. Ren, H.-Y.; Zhuang, D.-F.; Pan, J.-J.; Shi, X.-Z.; Wang, H.-J. Hyper-spectral remote sensing to monitor vegetation stress. J. Soil Sediment 2008, 8, 323–326. [Google Scholar] [CrossRef]
25. Milton, N.; Ager, C.; Eiswerth, B.; Power, M. Arsenic-and selenium-induced changes in spectral reflectance and morphology of soybean plants. Remote Sens. Environ. 1989, 30, 263–269. [Google Scholar] [CrossRef]
26. Kabata-Pendias, A.; Pendias, H. Trace Element in Soil and Plants; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
27. Wessman, C.A. Estimating canopy biochemistry through imaging spectrometry. In Imaging Spectrometry—A Tool for Environmental Observations; Hill, J., Megier, J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; pp. 57–69. [Google Scholar]
28. Nagajyoti, P.; Lee, K.; Sreekanth, T. Heavy metals, occurrence and toxicity for plants: A review. Environ. Chem. Lett. 2010, 8, 199–216. [Google Scholar] [CrossRef]
29. Chi, G.; Chen, X.; Shi, Y.; Liu, X. Spectral response of rice (Oryza sativa L.) leaves to Fe²⁺ stress. Sci. China Ser. C-Life Sci. 2009, 52, 747–753. [Google Scholar] [CrossRef] [PubMed]
30. Filella, I.; Serrano, L.; Serra, J.; Penuelas, J. Evaluating wheat nitrogen status with canopy reflectance indices and discriminant analysis. Crop Sci. 1995, 35, 1400–1405. [Google Scholar] [CrossRef]
31. Liu, M.; Liu, X.; Li, T.; Xiu, L. Analysis of hyperspectral singularity of rice under Zn pollution stress. Trans. CSAE 2010, 26, 191–197. (In Chinese) [Google Scholar]
32. Kaewpijit, S.; Le Moigne, J.; El-Ghazawi, T. Automatic reduction of hyperspectral imagery using wavelet spectral analysis. IEEE Trans. Geosci. Remote Sens. 2003, 41, 863–871. [Google Scholar] [CrossRef]
33. Misiti, M.; Misiti, Y.; Oppenheim, G.; Poggi, J.-M. Matlab Wavelet Toolbox User's Guide Version 3; The MathWorks, Inc.: Natick, MA, USA, 2004. [Google Scholar]
34. Graps, A. An introduction to wavelets. IEEE Comput. Sci. Eng. 1995, 2, 50–61. [Google Scholar] [CrossRef]
35. Schmidt, K.; Skidmore, A. Smoothing vegetation spectra with wavelets. Int. J. Remote Sens. 2004, 25, 1167–1184. [Google Scholar] [CrossRef]
36. Bruce, L.M.; Koger, C.H.; Li, J. Dimensionality reduction of hyperspectral data using discrete wavelet transform feature extraction. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2331–2338. [Google Scholar] [CrossRef]
37. Kingsbury, N. Image processing with complex wavelets. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1999, 357, 2543–2560. [Google Scholar] [CrossRef]
38. Koger, C.H.; Bruce, L.M.; Shaw, D.R.; Reddy, K.N. Wavelet analysis of hyperspectral reflectance data for detecting pitted morningglory (Ipomoea lacunosa) in soybean (Glycine max). Remote Sens. Environ. 2003, 86, 108–119. [Google Scholar] [CrossRef]
39. Pu, R.; Gong, P. Wavelet transform applied to EO-1 hyperspectral data for forest LAI and crown closure mapping. Remote Sens. Environ. 2004, 91, 212–224. [Google Scholar] [CrossRef]
40. Blackburn, G.A. Wavelet decomposition of hyperspectral data: A novel approach to quantifying pigment concentrations in vegetation. Int. J. Remote Sens. 2007, 28, 2831–2855. [Google Scholar] [CrossRef]
41. Zhang, J.; Lu, J. Feeding ecology of two wintering geese species at Poyang Lake, China. J. Freshw. Ecol. 1999, 14, 439–445. [Google Scholar] [CrossRef]
42. Luo, M.; Li, J.; Cao, W.; Wang, M. Study of heavy metal speciation in branch sediments of Poyang Lake. J. Environ. Sci. 2008, 20, 161–166. [Google Scholar] [CrossRef]
43. Uddling, J.; Gelang-Alfredsson, J.; Piikki, K.; Pleijel, H. Evaluating the relationship between leaf chlorophyll concentration and SPAD-502 chlorophyll meter readings. Photosynth. Res. 2007, 91, 37–46. [Google Scholar] [CrossRef] [PubMed]
44. Tokalioǧlu, Ş.; Kartal, Ş.; Elci, L. Determination of heavy metals and their speciation in lake sediments by flame atomic absorption spectrometry after a four-stage sequential extraction procedure. Anal. Chim. Acta 2000, 413, 33–40. [Google Scholar] [CrossRef]
45. Rafiee, J.; Tse, P.; Harifi, A.; Sadeghi, M. A novel technique for selecting mother wavelet function using an intelligent fault diagnosis system. Expert Syst. Appl. 2009, 36, 4862–4875. [Google Scholar] [CrossRef]
46. Lhermitte, S.; Verbesselt, J.; Verstraeten, W.; Coppin, P. A comparison of time series similarity measures for classification and change detection of ecosystem dynamics. Remote Sens. Environ. 2011, 115, 3129–3152. [Google Scholar] [CrossRef]
47. Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
48. Williams, P. Near-Infrared Technology: Getting the Best Out of Light: A Short Course in the Practical Implementation of Near-Infrared Spectroscopy for the User; Value Added Wheat CRC: Sydney, NSW, Australia, 2004. [Google Scholar]
49. Saeys, W.; Mouazen, A.M.; Ramon, H. Potential for onsite and online analysis of pig manure using visible and near infrared reflectance spectroscopy. Biosyst. Eng. 2005, 91, 393–402. [Google Scholar] [CrossRef]

© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).

corlisbutioncerhat.blogspot.com

Source: https://www.mdpi.com/2072-4292/7/11/15340/htm

Share :